Cours disponibles
Catégorie: Semestre 7
EM7MS200 (semestre 7) L’objectif est d’établir les différents concepts de la mécanique des solides déformables. Les différents tenseurs de déformations et de contraintes sont définis dans le cas des transformations finies. Le cas classique des transformations infinitésimales est traité…
Catégorie: Semestre 7
Les sujets des TP sont récupérables dans le module FS102 - TP de mécanique.
Catégorie: Semestre 7
Ce module a pour but de donner aux étudiants les bases de la programmation en C++, et d'acquérir une bonne maîtrise de ce langage pour des applications en calcul scientifique. Les premiers travaux pratiques permettront aux étudiants de se familiariser avec la programmation orientée objet et le…
Catégorie: Semestre 7
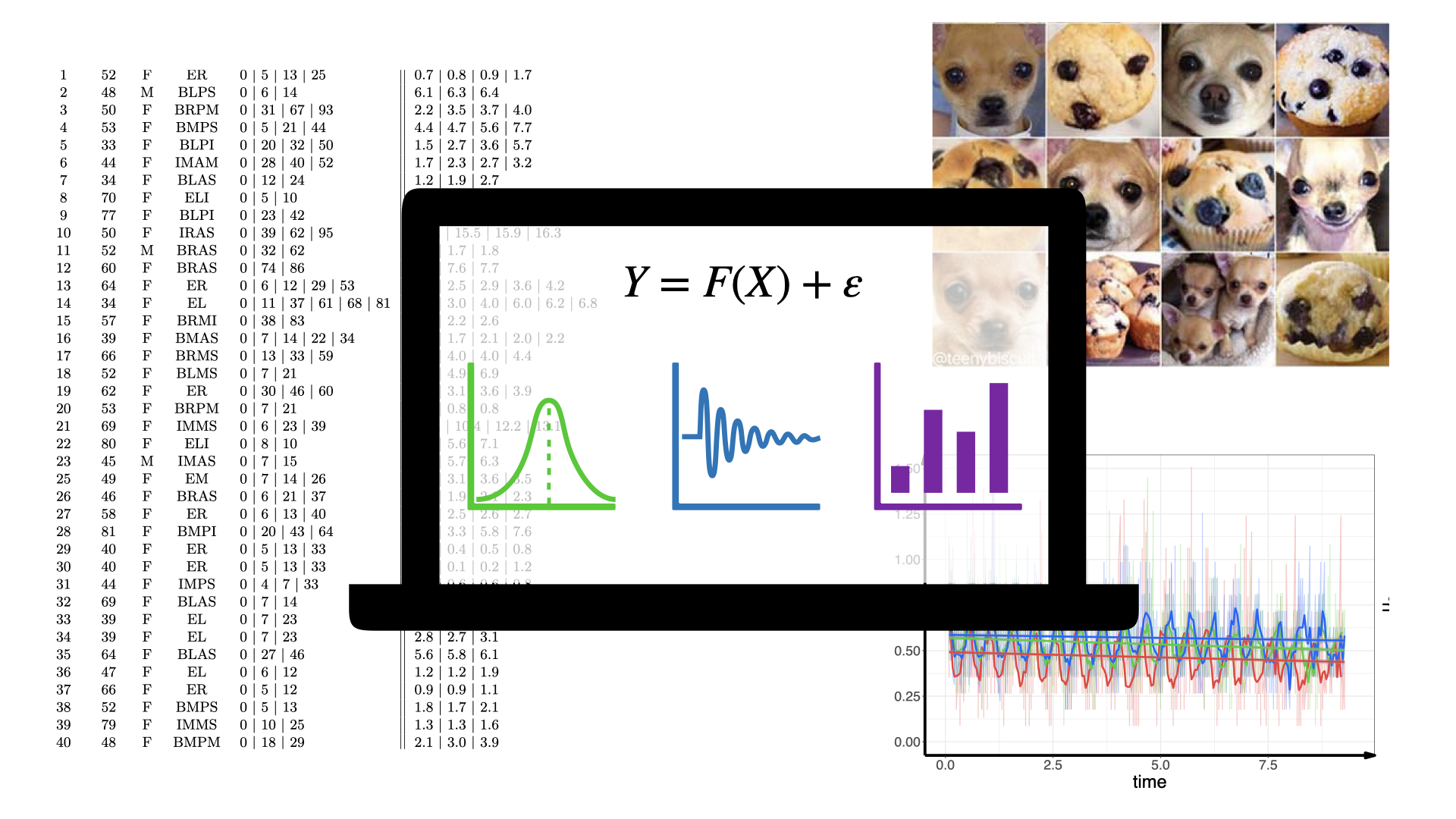
Dans ce cours dans une première partie, nous aborderons différentes techniques d’apprentissage statistique. Plus précisément nous nous intéresserons à l'apprentissage non supervisé avec les méthodes d’analyse en composantes principales et de partitionnement et à l'apprentissage supervi…
Catégorie: Semestre 7
L'objectif de ce cours est de présenter les méthodes itératives utilisées pour approcher les solutions de gros systèmes linéaire ou obtenir des éléments propres. On considérera des systèmes linéaires issus de problèmes en mécanique des structures ou des fluides. La plupart des méthode…